Indexing
TileDB implements super optimized, multi-dimensional slicing with the use of indexing. This section explains indexing in dense and sparse arrays separately. Visit the Storage Format Spec section for information on how TileDB implements indexing on storage, and the Key Concepts: Reads section to learn about how TileDB leverages indexing during the read operations.
Dense arrays
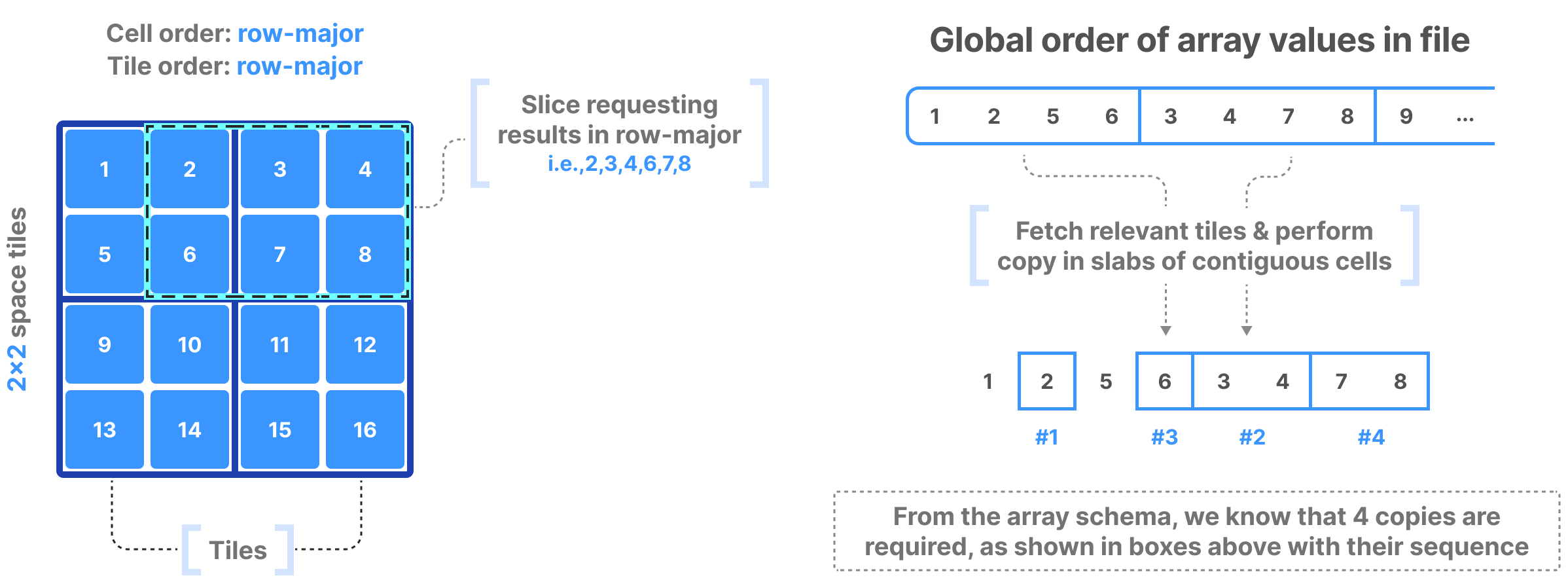
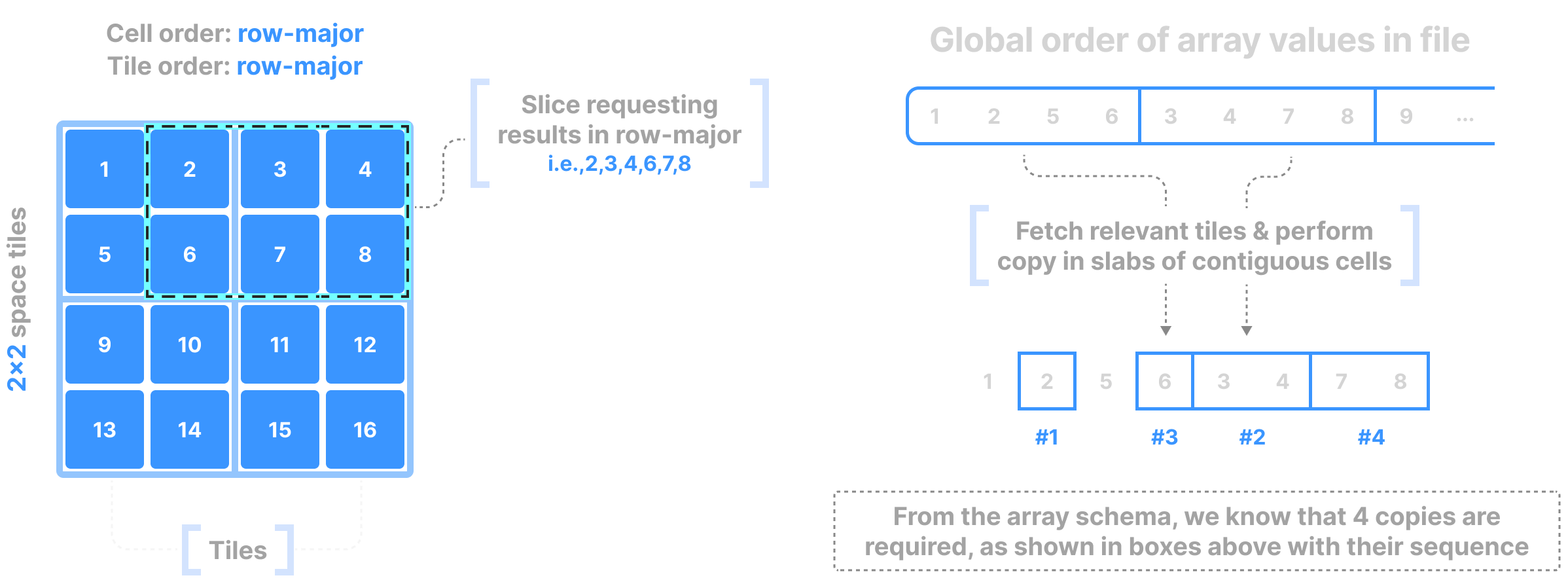
The following figure shows an example of dense array indexing. Along with the slicing information returned by the query, you know the following from the array schema: the number of dimensions, the global order, the tiling, and the fact that no empty cells exist in the array. Using solely the array schema and with basic arithmetic, you can calculate the number, size, and location of cell slabs (that is, sets of contiguous cells on disk) that form the query result, without any extra index. TileDB applies an efficient, multi-threaded algorithm that can fetch the relevant tiles from disk, decompress, and copy the cell slabs into the result buffers, all in parallel.
Sparse arrays
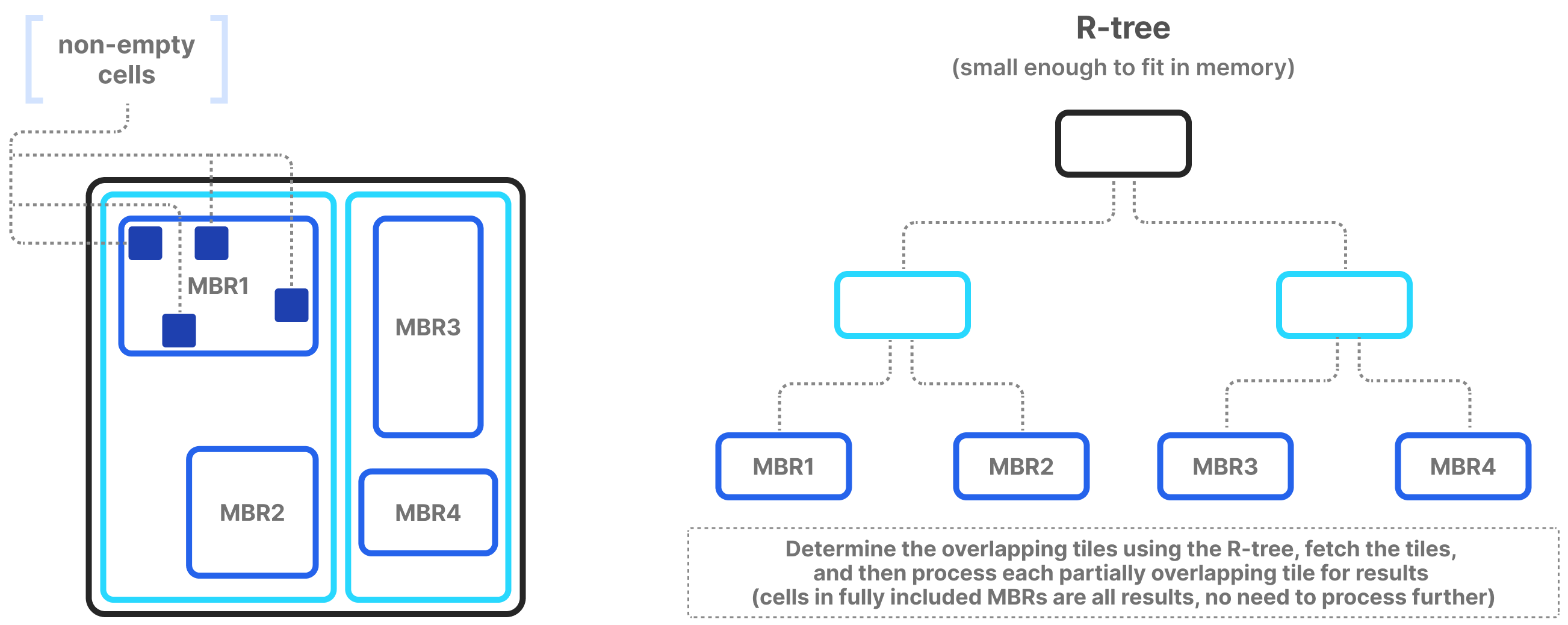
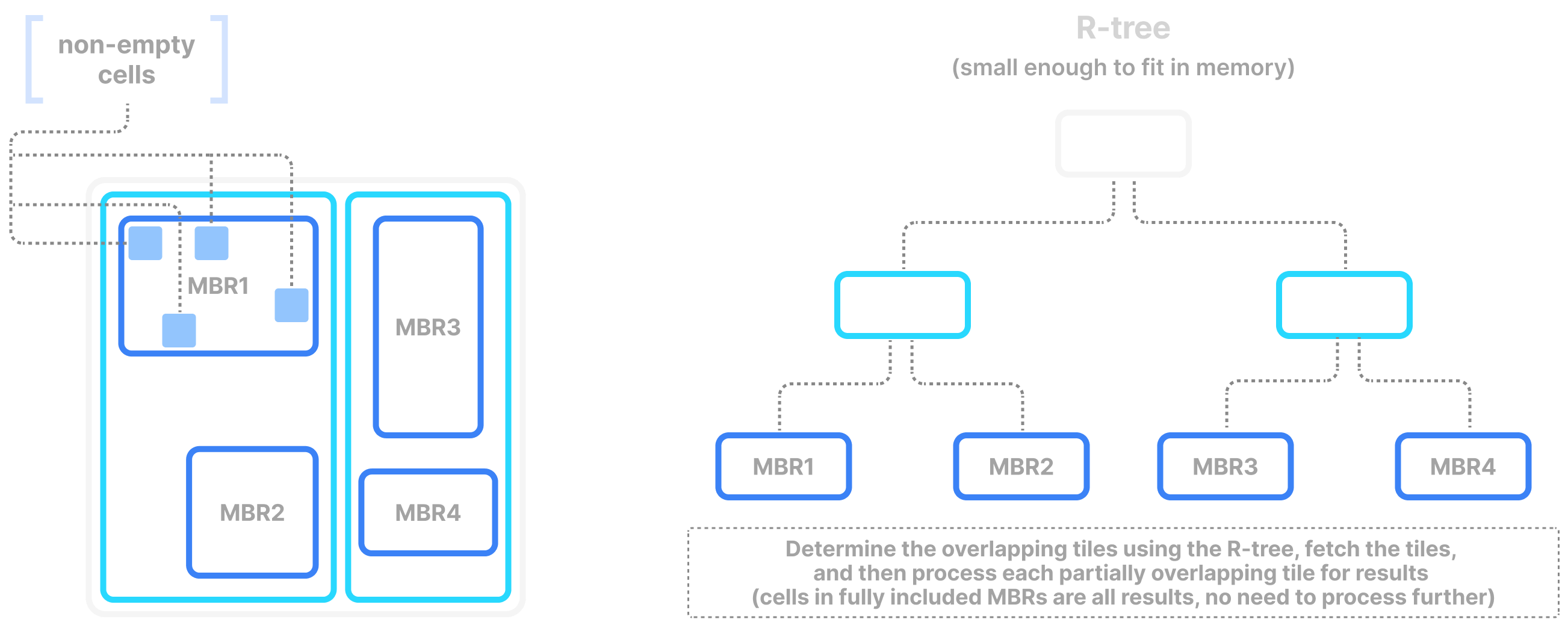
Slicing in sparse arrays is more difficult, because you do not know the location of empty cells until the array is written. Therefore, unlike dense arrays, TileDB needs to explicitly store the coordinates of the non-empty cells, and build an index on top of them. The index must be small in size so that it can be quickly loaded in main memory when the query is submitted. TileDB uses an R-tree as an index. The R-tree groups the coordinates of the non-empty cells into minimum bounding rectangles (MBRs), one per tile, and then recursively groups those MBRs into a tree structure. The figure below shows an example. The slicing algorithm then traverses the R-tree to find which tile MBRs overlap the query, fetches in parallel those tiles from storage, and decompresses them. Then, for every partially overlapping tile, the algorithm needs to further check the coordinates one by one to determine whether they fall inside the query slice. TileDB implements this simple algorithm with multi-threading and vectorization, leading to extremely efficient multi-dimensional slicing in sparse arrays.