Distance Metrics

Learn about the supported distance metrics in TileDB’s vector search functionality.

TileDB offers a variety of distance metrics for vector search. The distance metric is a key component of the vector search functionality, as it defines the similarity between vectors. This document explores the supported distance metrics and their formulas, and it provides visual representations.

Supported distance metrics

TileDB supports the following distance metrics:

Sum of squares distance (Squared Euclidean distance)
Euclidean distance (L2)
Inner product (dot product)
Cosine distance

The following sections explore each of these in detail.

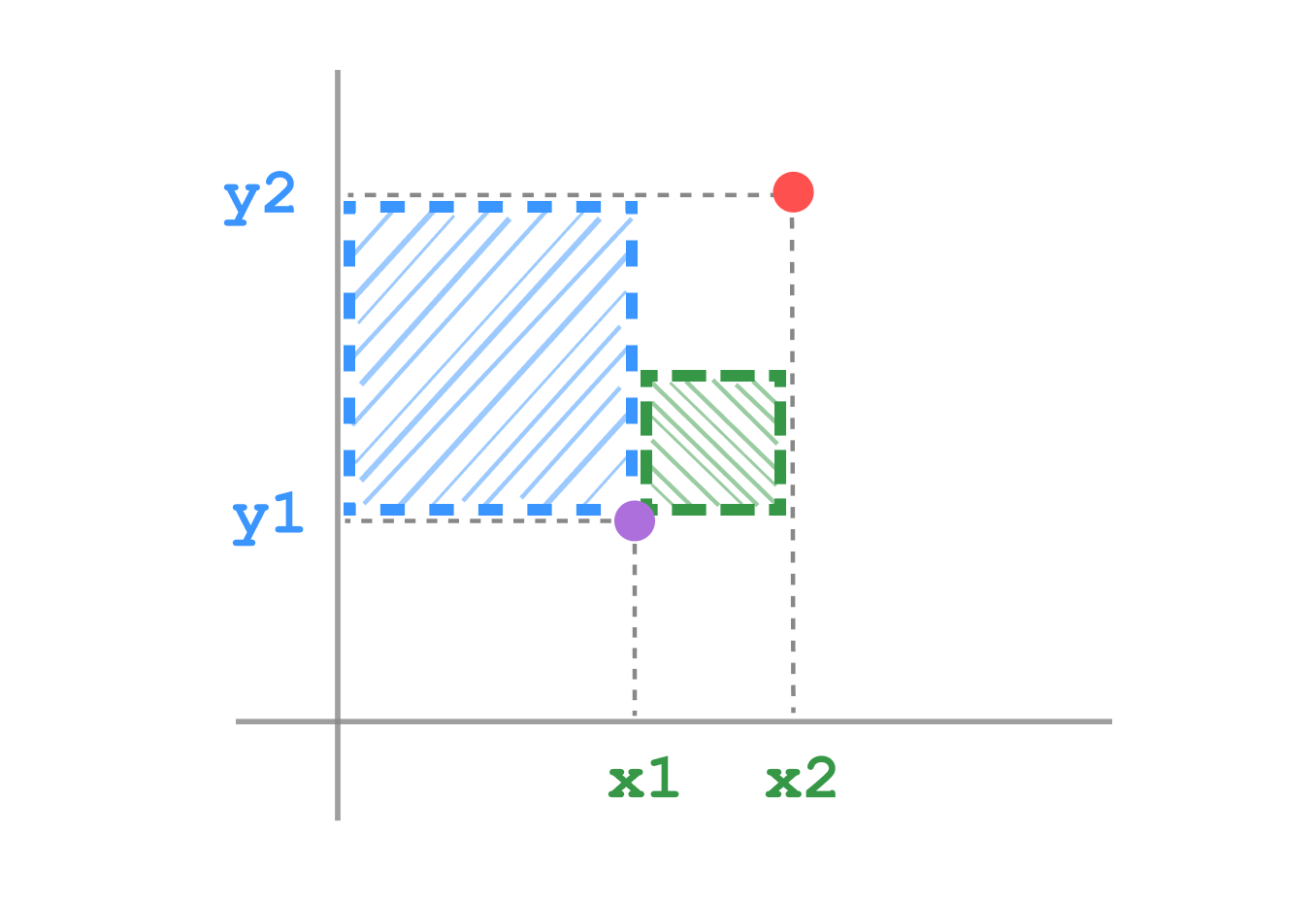
Sum of squares distance

Sum of squares distance, also known as Squared Euclidean distance, is the sum of the squared differences between corresponding elements of two vectors.

Note: the sum of squares metric results in the same ordering as the L2 metric but it is faster computationally as it skips the internal square root computation.

Formula

\[ d(x, y) = \sum_{i=1}^n (x_i - y_i)^2 \]

Where \(x\) and \(y\) are vectors, and \(x_i\) and \(y_i\) are their respective components.

Visualization

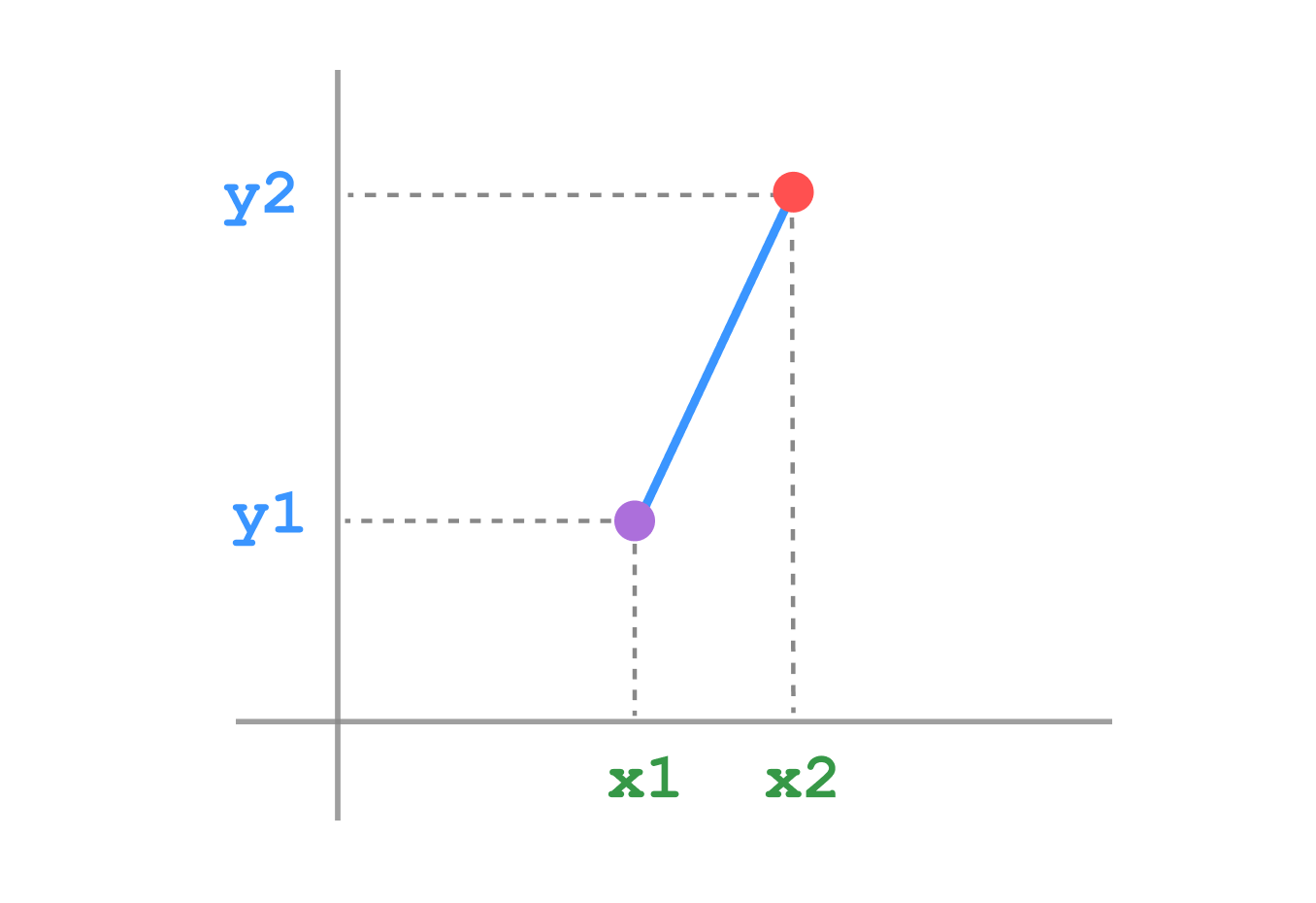
Euclidean distance

Euclidean distance is the “ordinary” straight-line distance between two points in Euclidean space. It’s the square root of the sum of squares distance.

Formula

\[ d(x, y) = \sqrt{\sum_{i=1}^n (x_i - y_i)^2} \]

Visualization

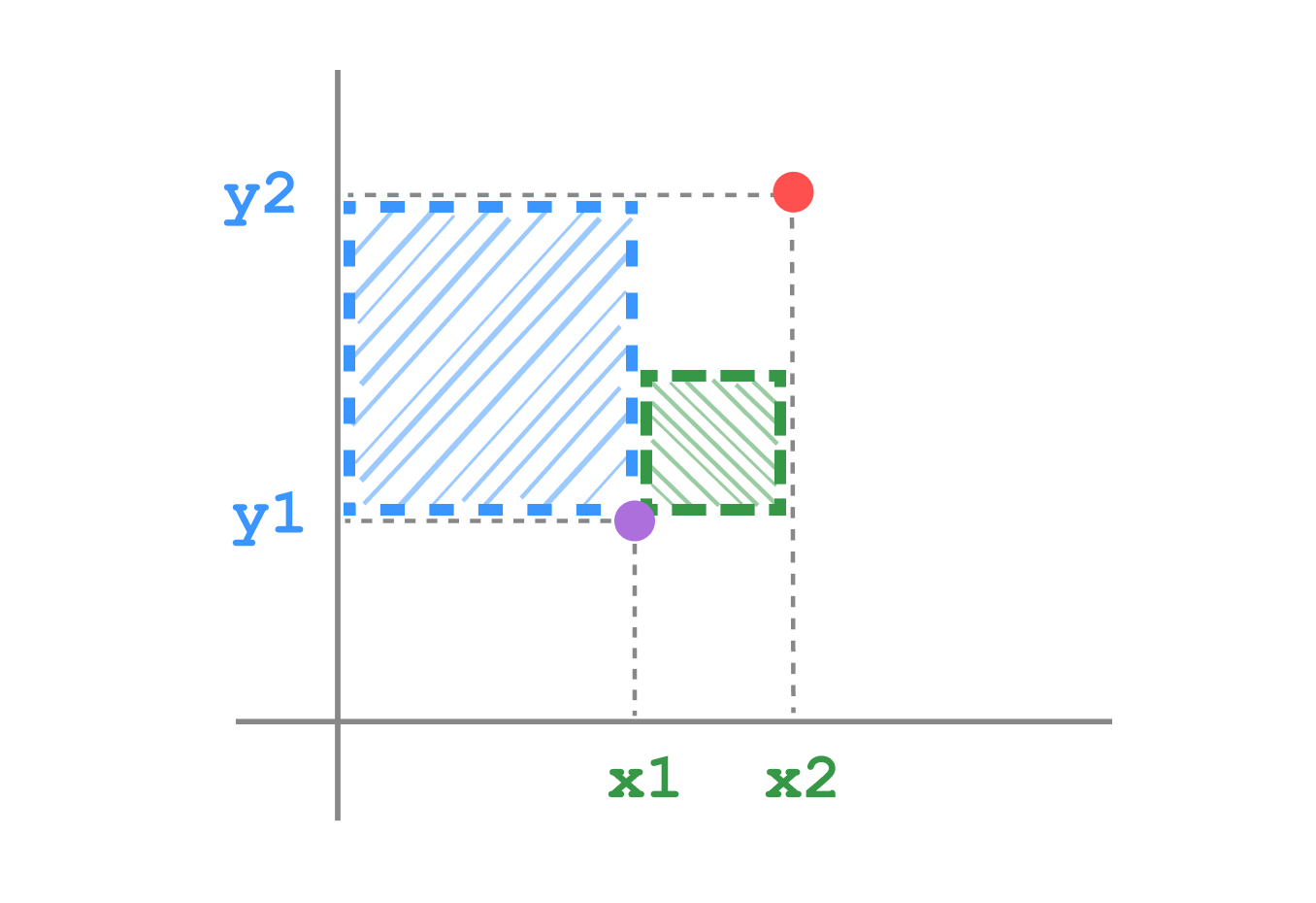
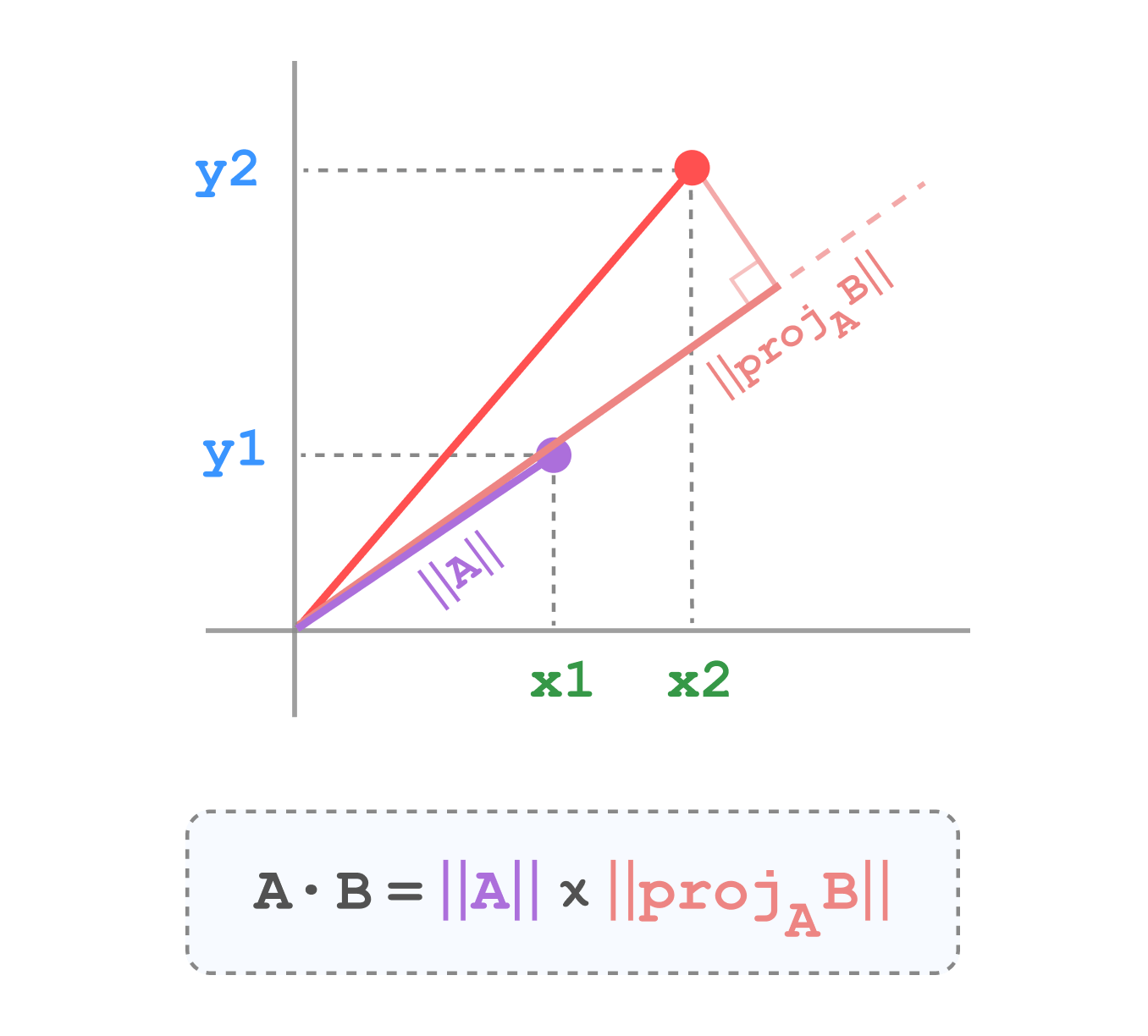
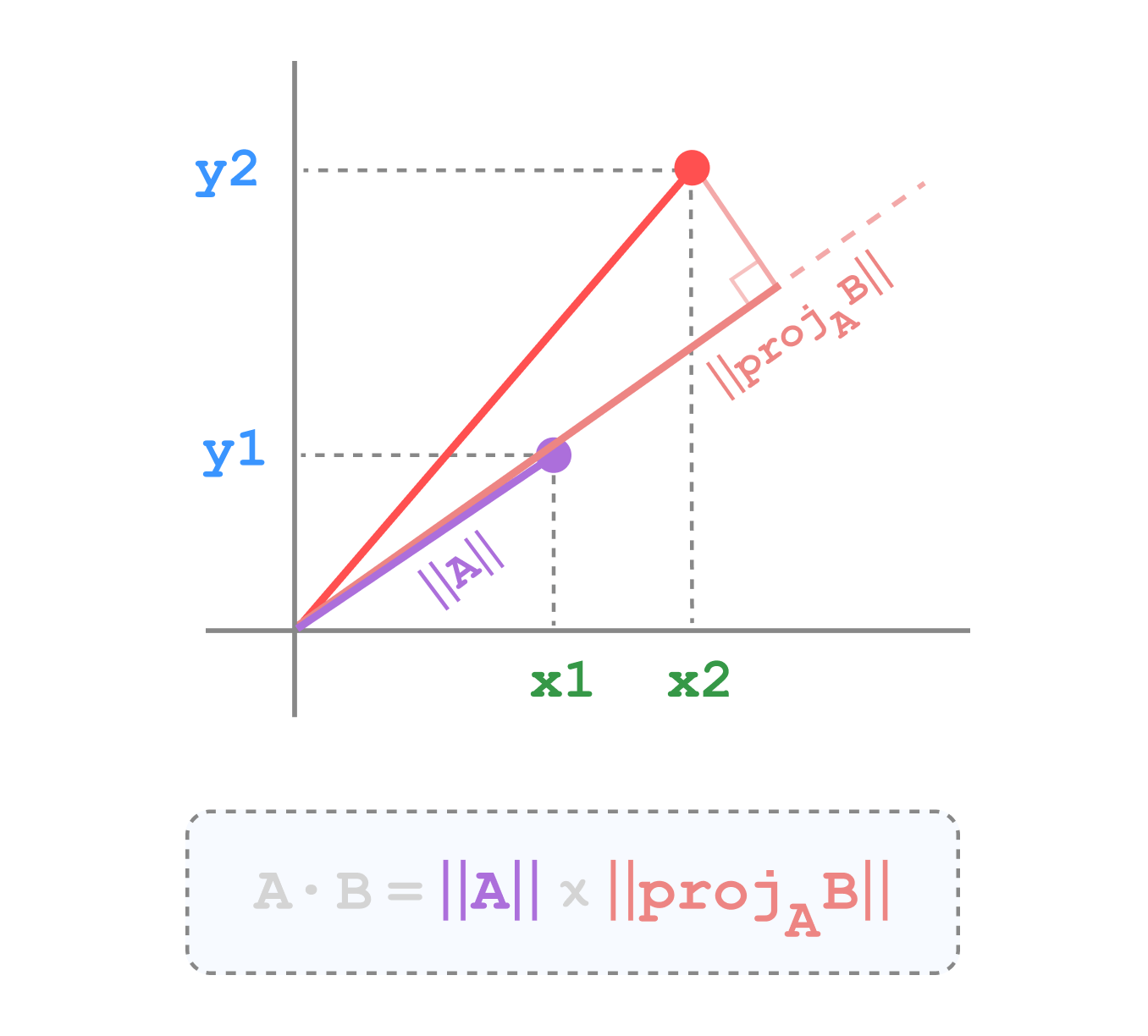
Inner product

Inner product, or dot product, measures the cosine of the angle between two vectors, multiplied by their magnitudes. It’s often used when the magnitude of the vectors is important.

Formula

\[ d(x, y) = x \cdot y = \sum_{i=1}^n x_i y_i \]

Visualization

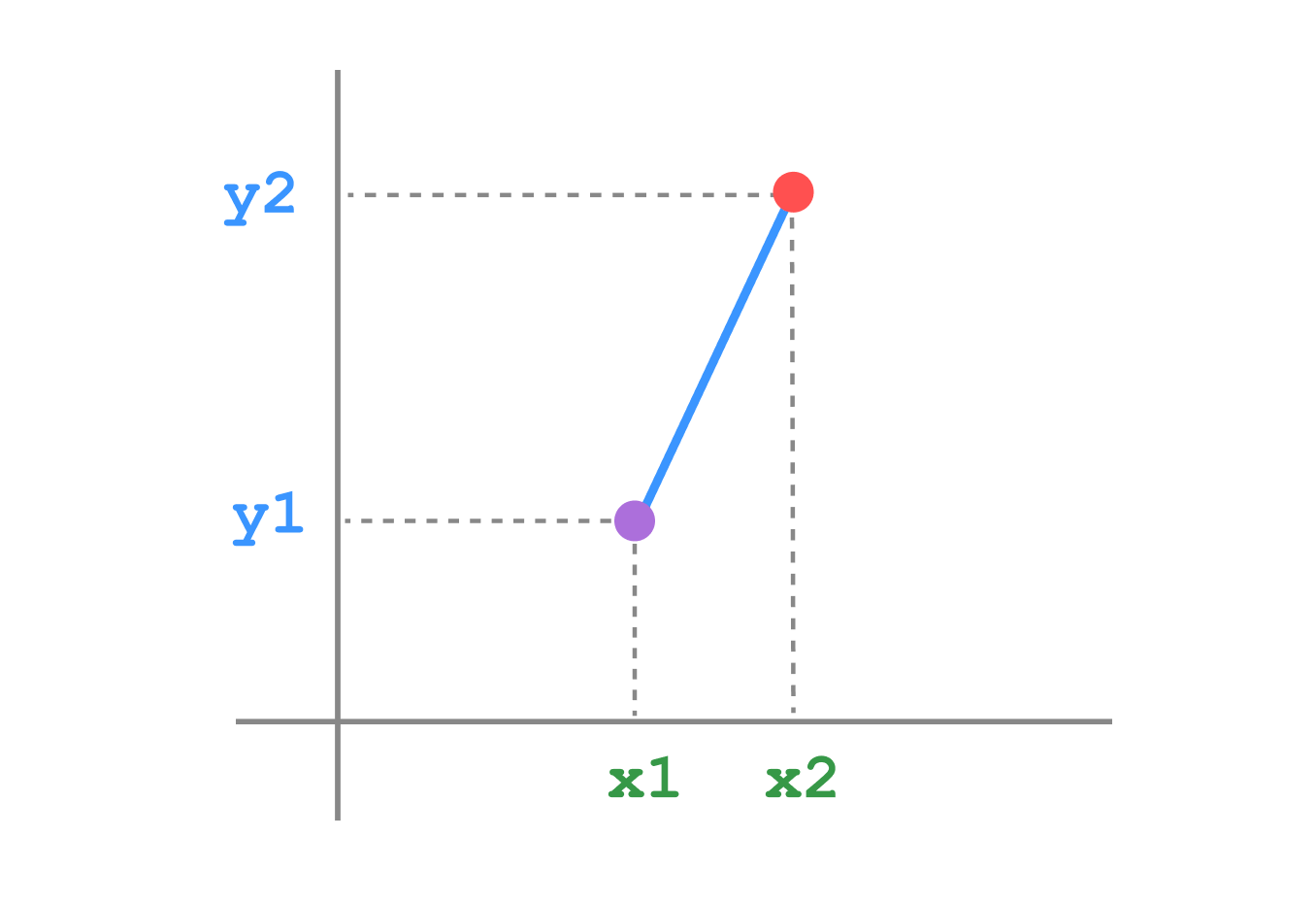
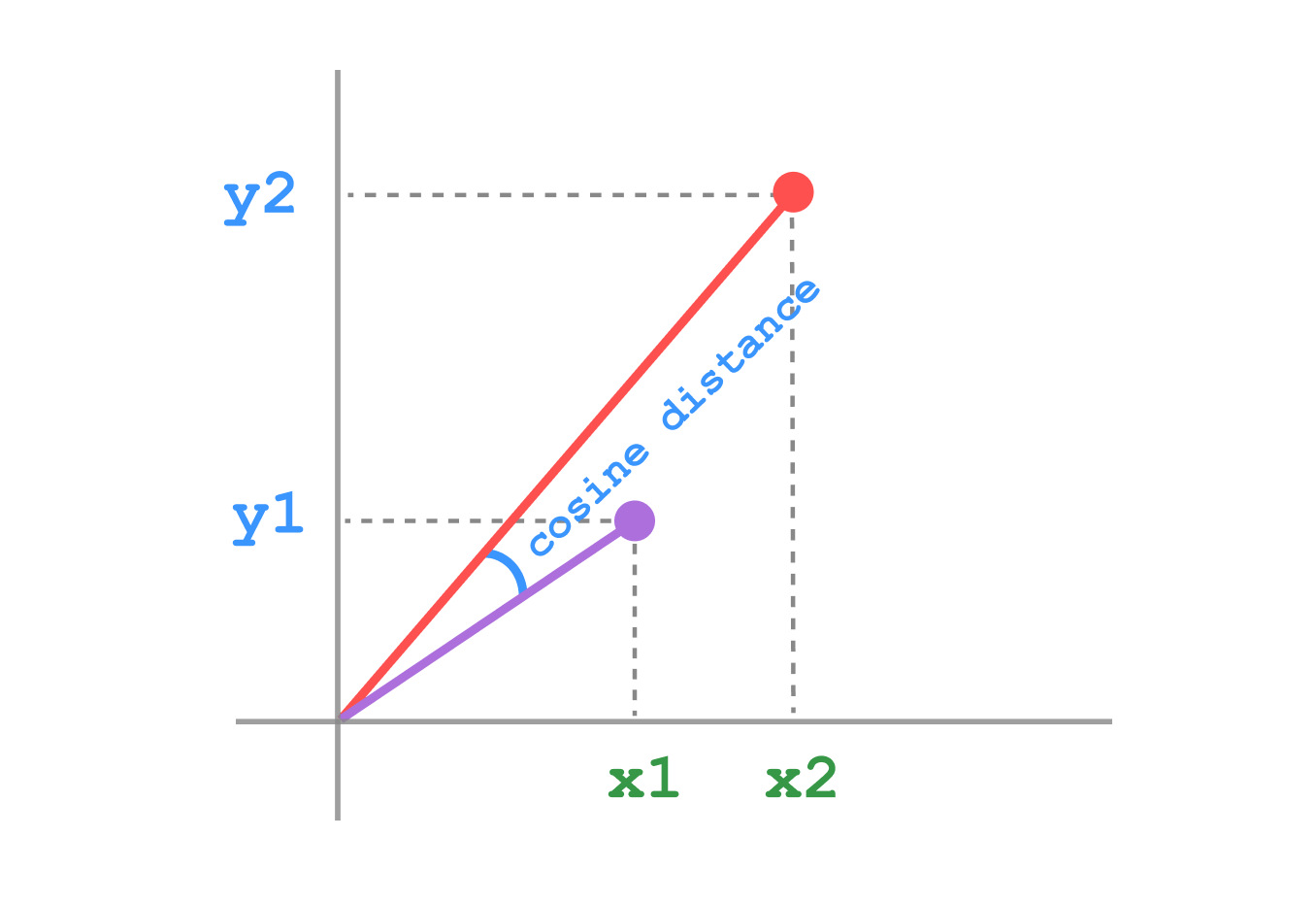
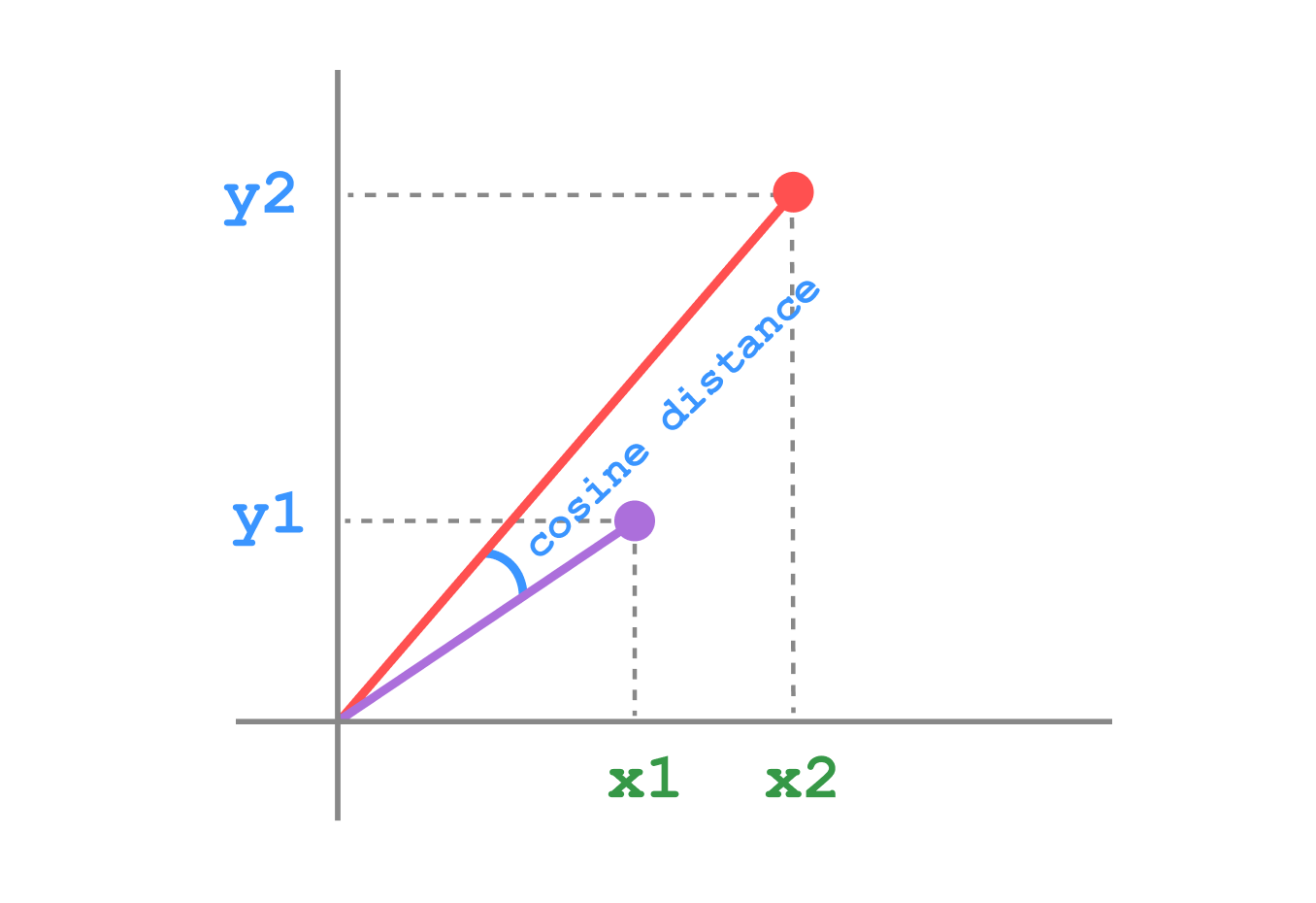
Cosine distance

Cosine distance measures the cosine of the angle between two vectors, ignoring their magnitudes. It’s particularly useful when dealing with high-dimensional data.

Formula

\[ d(x, y) = 1 - \frac{x \cdot y}{||x|| \cdot ||y||} \]

Where \(||x||\) and \(||y||\) are the magnitudes (Euclidean norms) of vectors \(x\) and \(y\).

Visualization

Index algorithm and distance metric compatibility

Index Algorithm	Sum of Squares	Euclidean	Inner Product	Cosine
`FLAT`	✅	✅	✅	✅
`IVF_FLAT`	✅	✅	❌	✅
`VAMANA`	✅	✅	❌	✅

Create an index with a specific distance metric

When creating a vector search index, you can specify the distance metric using the distance_metric parameter in the ingest or create functions.

from tiledb.vector_search import ingest
from tiledb.vector_search import _tiledbvspy as vspy

index = ingest(
    index_type="IVF_FLAT",
    index_uri="path/to/index",
    input_vectors=input_vectors,
    distance_metric=vspy.DistanceMetric.COSINE,
    partitions=10,
)

The vspy.DistanceMetric enum provides the following options:

vspy.DistanceMetric.SUM_OF_SQUARES
vspy.DistanceMetric.L2
vspy.DistanceMetric.INNER_PRODUCT
vspy.DistanceMetric.COSINE

Cosine distance normalization

When using the cosine distance metric, TileDB-Vector-Search normalizes the vectors before indexing. This normalization happens automatically during the index creation process.

However, if your dataset is already normalized, you can disable the extra normalization step by setting normalized=True in the ingest function.

Query with distance metrics

When querying an index, the distance metric used during index creation will be applied automatically:

distances, ids = index.query(query_vectors, k=5)

The returned distances will be calculated using the metric specified during index creation.

Conclusion

Understanding these distance metrics is crucial for effective vector search in TileDB. Each metric has its strengths and is suited for different types of data and applications. When implementing vector search, consider the nature of your data and the specific requirements of your application to choose the most appropriate distance metric.